Heap Data Structure

It appears I have forgotten the purpose of a heap. At the moment, I remember that heaps efficiently store a binary tree as some sort of array internally. The purpose of the binary tree is to optimize the insertion/reading/deletion of values by maintaining some sort of important information is readily accessible—most often the min/max of an array of numbers.

Common Misconception: The heap data structure has nothing to do with the heap in runtime memory, the region used for dynamic memory allocation.

The definition

A heap maintains 2 properties:

1. Complete Binary Tree - Every level is filled, except possibly the last where it is filled left to right
2. Heap Property - For a max-heap, every parent is greater than or equal to its children. For a min-heap, every parent is less than or equal to its children.

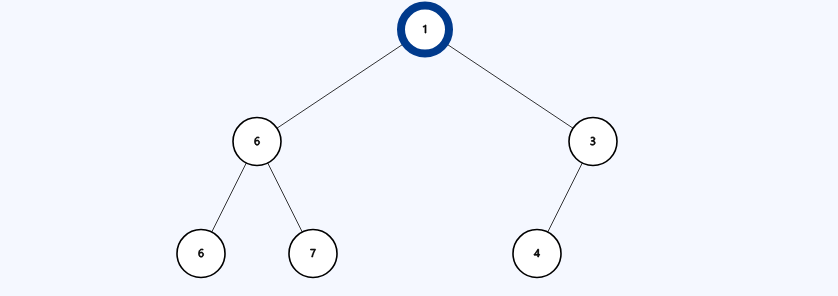
Common Misconception: The heap property does not guarantee any sort of ordering beyond the heap property. Notice how in the following min-heap tree (stored as [1, 6, 3, 6, 7, 4]), the children of the root are backwards? Additionally, 6 is a child of the root rather than 4 which is clearly smaller, yet the heap-property is still maintained.

The benefit

The beauty of a heap comes from maintaining efficient O(1) access to some important element, generally the min/max from some set of comparable values.

Additionally, insertion/deletion will take O(logn) by percolating up/down the tree to maintain the heap property which is very optimal.

Some use cases:

• Priority queue - Are largely built on top of heaps
• Streaming k largest/smallest elements, not just the min/max

The structure

It turns out the array logic is quite simple, for a node at index i, the left child is at 2i + 1 and the right child at 2i + 2. The parent can be found at (i - 1) / 2.